Disjoint Set이란?
Disjoint Set을 번역하면 서로소 집합입니다. 이는 공통된 원소를 가지고 있지 않는 집합들을 표현하는 자료 구조 입니다. 즉, 교집합이 공집합이고, 상호배타적입니다.
https://ko.wikipedia.org/wiki/%EC%84%9C%EB%A1%9C%EC%86%8C_%EC%A7%91%ED%95%A9
서로소 집합 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 집합론에서 서로소 집합(-素集合, 영어: disjoint sets)는 공통 원소가 없는 두 집합이다.[1] 예를 들어서 {1, 2, 3}과 {4, 5, 6}은 서로소이며 {1, 2, 3}과 {3, 4, 5}는 아니다.
ko.wikipedia.org
어떻게 표현하나?
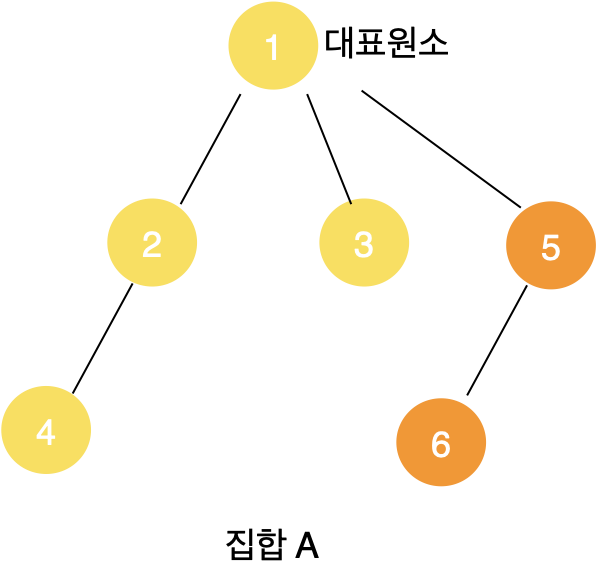
기본적인 원리는, 각 집합들을 트리로 구성해서 Root 노드를 대표 원소로 만드는 것입니다. 즉, 하나의 트리에 있는 모든 원소들은 하나의 대표 원소(Root 노드)를 가지게 됩니다. 따라서, 두 원소의 대표원소를 구하여 두 원소가 같은 집합에 있는지 판단할 수 있습니다.

Find
이 자료구조는 Union-Find라고도 불리는데요, 두 집합을 하나의 집합으로 합치는 Union과 대표원소를 찾는 Find, 두 가지 기능으로 이뤄져있기 때문입니다. 그 중에서 Find를 먼저 알아보겠습니다.
대표원소 찾는 것은 Root노드를 찾는 것입니다. 즉, 트리를 구현하는 방법에 따라서 달라질 수 있습니다. Union-Find에서는 주로 트리를 부모 노드를 표현하는 배열로 구현합니다. 예를 들어, 위의 집합들은 아래와 같이 표현될 수 있습니다.
| 원소 | 1 | 2 | 3 | 4 | 5 | 6 |
| 부모 원소 |
1 | 1 | 1 | 2 | 5 | 5 |
그리고 재귀적으로 원소 번호와 부모원소가 일치할 때까지 탐색합니다. 예를 들어 원소4의 대표원소를 찾는다면, 아래와 같은 식입니다.
4의 부모 원소 2
2의 부모 원소 1
1의 부모 원소 1 => 대표 원소
그런데 위와 같은 방법은 skewed tree인 경우 Find를 1회 수행하기위해 O(N)만큼의 시간 복잡도가 소요됩니다.
이를 좀더 빠르게 하기 위해 최적화합니다. 사실, 위의 트리에서 중요한 것은 '루트 노드'입니다. 따라서, find를 진행할 때마다, 각 부모 원소들을 아래와 같이 바꿔줄 수 있습니다.
| 원소 | 1 | 2 | 3 | 4 | 5 | 6 |
| 부모 원소 |
1 | 1 | 1 | 1 | 5 | 5 |
그러면 최적화된 find의 경우 O(1)로 대표원소를 찾을 수 있습니다. 하지만, 실재 이 구조를 이용할 경우, 최적화된 것과 그렇지 않은 것이 혼재되어 있기 때문에 정확한 시간복잡도를 계산하는 것이 어렵지만, 훌륭하신 분들에 의하면 O(α(N))라고 하며, 거의 상수와 비슷하다고 합니다.
Union
다음으로 다룰 것은 두 집합을 합치는 Union입니다. 이것은 두 집합의 대표 노드를 아래와 같이 하나로 일치시키면 됩니다.
그런데 여기서 중요한 것은 트리가 사향이 되는 것을 방지하기 위한 규칙입니다. 이것은 각 집합의 깊이를 기준으로 합니다. 두 집합 중 깊이가 더 낮은 집합이 큰 집합으로 편입되는 방식입니다.
여기서는 정확한 깊이의 값이 아닌, 대소만 구분하면 되기 때문에 깊이 대신 rank로 표시를 해두고, 두 대표원소의 rank가 같은 경우에만 편입 당하는 (대표원소가 유지되는) 쪽의 대표원소의 랭크를 +1 해주면됩니다.
다시 정리하면 Union은,
각 원소의 대표원소를 찾은 후,
대표 원소의 랭크를 비교해서,
더 낮은 쪽이 높은 쪽으로 편입하고( = 낮은 쪽의 대표원소의 부모원소를 높은 쪽의 대표원소로 치환하고),
두 랭크가 같다면, 한쪽 원소의 랭크를 +1한 후, 더 낮은 쪽이 높은 쪽으로 편입합니다.
Union의 시간복잡도는, 각 원소의 대표원소를 찾는 find에 의존함으로 O(α(N))입니다.
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] 비트마스킹 (0) | 2023.01.26 |
|---|---|
| [알고리즘] 플로이드-워셜 (Floyd-Washall) (0) | 2023.01.20 |
| [알고리즘] Kruskal 알고리즘 (feat. Union-Find) (0) | 2023.01.16 |
| [알고리즘] 위상 정렬 (0) | 2023.01.15 |
| [알고리즘] 누적합 (Prefix Sum) (0) | 2023.01.13 |